(Enem/2014) Um fabricante de cosméticos decide produzir três diferentes catálogos de seus produtos, visando a públicos distintos. Como alguns produtos estarão presentes em mais de um catálogo e ocupam uma página inteira, ele resolve fazer uma contagem para diminuir os gastos com originais de impressão. Os catálogos C1, C2 e C3 terão, respectivamente, 50, 45 e 40 páginas.
Comparando os projetos de cada catálogo, ele verifica que C1 e C2 terão 10 páginas em comum; C1 e C3 terão 6 páginas em comum; C2 e C3 terão 5 páginas em comum, das quais 4 também estarão em C1.
Efetuando os cálculos correspondentes, o fabricante concluiu que, para a montagem dos três catálogos, necessitará de um total de originais de impressão igual a:
A) 135
B) 126
C) 118
D) 114
E) 110
Resolução
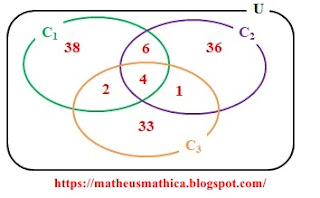
A questão é facilmente resolvida utilizando a teoria dos conjuntos. Assim, vamos montar o diagrama de Venn da seguinte forma:
Consideramos o seguinte diagrama:
Do texto, 4 páginas são comuns a C1, C2 e C3. Então colocamos o valor 4 no centro do diagrama.
C2 e C3 possuem 5 páginas em comum, no entanto, 4 delas também pertencem a C1. Sendo, portanto, apenas 1 página para a interseção de C2 e C3.
C1 e C2 possuem 10 páginas em comum sendo 4 delas também comuns a C3, logo restam 6 que são exclusivas a C1 e C2.
A mesma análise é feita para C1 e C3. Segundo o enunciado, 6 são comuns a essas duas, mas levando em conta as 4 comuns às três páginas restam duas.
O próximo passo é determinar as páginas que são exclusivas a cada catálogo. Fazemos isso subtraindo os valores das interseções do total de páginas de cada catálogo informado no enunciado, assim:
Em apenas C1 tem-se : 50 - 12 = 38
Em apenas C2 tem-se: 45 - 11 = 34
E em apenas C3 tem-se: 40 - 7 = 33
Dessa forma, podemos completar o diagrama.
O total de originais (U) é obtido somando todos os valores do diagrama, ou seja:
U=4 + 1 + 2 + 6 + 38 +34 + 33 = 118
Portanto, alternativa C é a correta.
Nenhum comentário:
Postar um comentário