Pérola da expansão

Autor da imagem: Desconhecido

Referência:

A caça - A Matemática na Mesopotâmia

As civilizações antigas da MESOPOTÂMIA são comumente chamadas de babilônicas, e nosso conhecimento sobre a matemática tem como fonte diversas tábuas em argilas gravadas em escrita CUNEIFORME, que chegaram aos nossos dias. Cerca de metade dos problemas contidos nas tábuas são puramente aritméticos (ou algébricos) e GEOMÉTRICOS, e dizem respeito, normalmente a problemas sobre áreas ou VOLUMES que envolvem a descoberta de INCÓGNITAS. Ao contrário da maioria das civilizações o sistema numérico mesopotâmico tinha como base o valor SESSENTA. Até hoje, o sucesso desse sistema se reflete em nossas unidades de TEMPO e medida de ÂNGULOS.
Aos babilônios se deve a invenção do sistema POSICIONAL. Com apenas seus símbolos para unidades e dezenas, podiam representar qualquer número, por maior que fosse por repetição e mudança de posição. Este é o mesmo princípio de nosso sistema numeral. Não havia notação para ZERO, embora às vezes deixassem um espaço em branco para indicar zero, o que gerava algumas confusões. Criou-se, mais tarde, um símbolo para zero, mas que só era usado em posições intermediárias. 
Os babilônios deram algumas aproximações interessantes de raízes quadradas de números que não são QUADRADOS perfeitos. Dentre as tábuas matemáticas babilônicas encontramos a chamada PLIMPTON escrita aproximadamente entre 1900 e 1600 a.C.. Ela consiste de três colunas praticamente completas de caracteres que contém ternas pitagóricas; isto é, números que representam a medida da HIPOTENUSA e de um cateto de triângulos retângulos cujos três lados têm medida inteira.

Encontre as palavras destacadas no texto:

Encontrou?

Teorema

Crispy Plotter

O Crispy Plotter é uma aplicação open-source que busca auxiliar estudantes, pesquisadores e curiosos que fazem uso de funções (simples ou complexas) no seu dia-a-dia.

Com o programa, além de se obter facilmente gráficos das mais diversas funções, é possível criar simulações auditivas de determinadas fórmulas, cujos gráficos lembram ondas sonoras, inclusive podendo gerar interferências através de vários gráficos.

Para comparação de resultados e análise de procedimentos, é possível plotar até 12 funções diferentes em um mesmo sistema cartesiano, sobrepondo os gráficos codificados por cor. Cada fórmula é descrita numa aba diferente, podendo ser editada rápida e facilmente. Após a plotagem, é possível também exportar os gráficos para arquivos de imagem raster no formato BMP, ou para vetores SVG e EMF.

4 é igual a 6?

Demonstração

 

Começamos com a seguinte igualdade:

-24 = -24

Escrevemos o número -24 em duas formas diferentes:

16 - 40 = 36 - 60

Os números 16, 40 , 36 e 60 podem ser escritos da seguinte forma:

4.4 - 2.4.5 = 6.6 - 2.6.5

Podemos somar 25 nos dois lados da equação sem a alterar:

4.4 - 2.4.5 + 5.5 = 6.6 - 2.6.5 + 5.5

Agora vemos que tanto no lado esquerdo como no lado direito temos um  quadrado de um binómio (o primeiro termo ao quadrado, menos duas vezes o produto dos dois termos mais o quadrado do segundo)
   
(4 - 5)²  = (6 - 5)²

Eliminando o quadrado nos dois lados da equação temos:

4 - 5 = 6 - 5

Finalmente, somando 5 nos dois lados, obtemos o resultado:

4 = 6

 c.q.d

Obviamente esta demonstração possui um erro, pois todos nós sabemos que 4 não é igual a 6 (ou alguém tem alguma dúvida?).




TENTE DESCOBRIR ONDE ESTA O ERRO !

Pi

Pi

Max (Sean Gullette), um jovem gênio da matemática e computação que vive escondido da luz do sol, que lhe dá constantes dores de cabeça, e evita o contato com outras pessoas é é capaz de realizar complicadas operações matemáticas de cabeça, em segundos, transformando-se na alegria de uma criança que mora no mesmo prédio que ele . Além de ser completamente obcecado pela matemática, ao ponto de ver números em qualquer lugar o  matemático dedicou sua vida a construir um supercomputador com poder para calcular padrões e variantes numéricas.

O único amigo do rapaz é um velho matemático, chamado Sol Robeson (Mark Margolis) que  jogava partidas de Go (um milenar jogo de tabuleiro oriental) com Max. Durante as partidas, ambos discutem suas teorias matemáticas.

 
Max conseguiu construir um supercomputador que lhe permitiu descobrir o número completo do pi, o que fez ainda com que compreendesse toda a existência da vida na Terra, já que percebeu que todos os eventos se repetiam após um determinado espaço de tempo. Com isso Max pôde adivinhar o que viria a acontecer no mercado da bolsa de valores, já que conhecia as tendências que se repetiriam, e passa a ser cobiçado por representantes de Wall Street e também por uma seita que busca decifrar os mistérios da matemática. Porém Max é aconselhado por Sol a tomar cuidado, pois sua pesquisa pode levá-lo a consequências muito graves.

Título original:Pi
Lançamento:1998(EUA) 
Direção: Darren Aronofsky
Atores: Sean Gullette; Mark Margolis; Ben Shenkman; Pamela Hart; Stephen Pearlman; Samia Shoaib; Ajay Naidu; Kristyn Mae-Anne Lao; Espher Lao Nieves.
Duração:85 min
Gênero:Ficção Científica


Trailer 

Elena Lucrezia Cornaro Piscopia

Elena Lucrezia Cornaro Piscopia (1646-1684)

Elena Lucrezia

Elena Lucrezia Cornaro Piscopia nasceu em uma família nobre em  1646 na Veneza, Italia. Seu pai, Giovanni Baptista Cornaro, era o Procurador de San Marco e altamente considerado. A mãe de Elena, Zanetta Giovanna Boni, não era membro de classe privilegiada antes da sua união. O pai de Elena gastou sua vida para estabelecer o nome de Cornaro, um nome que devesse ser recordado para sempre por causa do intelecto da sua filha mais velha.

Começando aos 7 anos de idade, Elena Piscopia recebeu o conhecimento das línguas clássicas do latin e do grego,estudando a gramática e a música. Além de falar latin e o grego fluentemente, Elena dominou hebreu, espanhol, francês, e o árabe. Seu domínio das línguas trouxe o título Oraculum Septilingue. Elena exibiu também poderes maravilhosos de raciocínio. Era uma estudante das ciências assim como das línguas, e estudou a matemática e a astronomia além da filosofia e da teologia. O grande amor de Elena era para com a filosofia e o teologia. Seu pai em 1672 a enviou à distinta Universidade de Pádua para continuar com seus estudos.

Elena não procurou graduação na universidade de Pádua; quis simplesmente continuar sua aprendizagem. Entretanto, Giovanni insistiu que o mundo reconhecesse o conhecimento incrível de sua filha. Assim, com sua insistência, Elena aplicou-se em um Doutorado de teologia na Universidade de Pádua. Elena encontrou resistência em seus estudo. Os oficiais da igreja católica romana recusaram conferenciar o título de Doutor em Teologia a uma mulher. Elena aplicou-se, outra vez, pela insistência do seu pai. Desta vez a igreja comprometeu-se e permitiu que Elena recebesse Doutorado em Filosofia.

A examinação de Elena para o doutorado em filosofia deveria ser realizado no salão da Universidade de Pádua, mas devido a quantidade de espectadores foi transferido para a catedral de Pádua. Durante todo sua examinação, as respostas brilhantes de Elena espantaram seus examinadores, que determinaram que seu vasto conhecimento superava o Doutorado de filosofia e, em 25 de junho de 1678 Elena recebeu o Doutorado de Filosofia da Universidade de Pádua. Aos 32 anos de idade era a primeira mulher no mundo a receber grau de doutorado. Além do grau do doutorado, Elena recebeu a capa de eminente professora, e coroa do laurel do poeta.

Aos 17 anos de idade Elena foi considerada perita em musica . Ela dominou vários instrumentos, entre eles: a harpa e o violino. Seu auge musical foi coroado pela música que compôs. Elena era membro estimada de vários academias em todo a Europa, e recebeu visitas de alunos de todas as partes do mundo. Elena apreciou lecionar, dando aulas de música, de teologia, e composição. Margaret Alic indica que ela se transformou em professora de matemática na universidade de Pádua em 1678. Seus escritos foram publicadas em 1688 em Parma, Italia após sua morte. Hoje os informes de Elena é citado extensamente por outros mestres e escritores.

Após ter recebido com sucesso seu grau da universidade de Pádua, Elena devotou sua vida a caridade. Abdicou seu lugar na sociedade e recusou diversas uniões importantes, usando o hábito da ordem das beneditinas. Durante os últimos sete anos de sua vida, Elena focalizou-se na aprendizagem e em ministrar aulas aos pobres. Elena morreu aos 32 anos de idade em 1684. Sua morte acreditasse que tenha sido causada pela tuberculose.

Referências:

http://www.agnesscott.edu/lriddle/women/piscopia.htm 

http://www.profgarcia.xpg.com.br/mulheresMatematicas.htm 

http://www.dec.ufcg.edu.br/biografias/ElenPisc.html 

Os gatos

Uma sala tem quatro cantos; cada canto tem o seu gato; cada gato vê três gatos… quantos gatos são?

As Botas

Bota e meia em cada pé, quantas botas são?

A palavra noite e o número 8.

Em quase todos os idiomas europeus, a palavra NOITE é formada pela letra N + o número 8.

A letra N é o símbolo matemático do infinito e o 8 deitado também simboliza isso, ou seja, noite significa a união do infinito. Vejamos:

Português: noite= n + oito

Inglês: night= n + eight

Alemão: ãcht= n + acht

Espanhol: noche= n + ocho

Francês: nuit= n + huit

Italiano: notte= n + otto

Aritmética da Emilia

O livro Aritmética da Emília é um típico livro do grande escritor José Bento Monteiro Lobato que traz como personagens o Visconde de Sabugosa, a Emília, a Narizinho, D. Benta, Tia Nastácia, Quindim, e o Rinoceronte que são os  inesquecíveis personagens do  Sítio do Picapau Amarelo.  Neste livro o autor demonstra uma maneira prática de ensinar e aprender Matemática usando a criatividade e a peripécia das personagens do Sítio.

Nas primeiras páginas do livro ele aborda a idéia do Visconde em ensinar as crianças  a Matemática formulando assim uma viagem ao País da Matemática, isto é, a viagem seria diferente era o país que viria até o Sítio. Como Visconde havia pensado em tudo a viagem aconteceu de verdade. Daí começa a bela história da Matemática tendo como orientador o Visconde.

Para explicar a história o visconde conta com a ajuda de artistas e colobarodores do país da Matemática. A cada entrada de determinado tema entram artistas diferentes e engraçados as crianças aprendem a Matemática de modo prático e divertido. Alguns conteúdos abordados no livro pelo autor são: Algarismos Arábicos e Romanos; Leitura e escrita de números; Ordens e Classes; Sistema Monetário; Sinais Aritméticos; Problemas; Frações; Mínimo Múltiplo Comum; Números Decimais e Complexos; e as Medidas.

Todos estes assuntos são explicados minuciosamente pelo personagem do Visconde de Sabugosa. O livro é um excelente convite ao estudo prazeroso da Matemática ele leva o leitor a vivenciar a viagem junto com as personagens. O livro é uma boa pedida  de leitura para crianças de séries inicias para desmistificar o medo da Matemática.

Editora: Globo
Autor: MONTEIRO LOBATO
ISBN: 9788525045942
Origem: Nacional
Ano: 2009
Edição: 1ª
Número de páginas: 128
Acabamento: Brochura
Formato: Médio

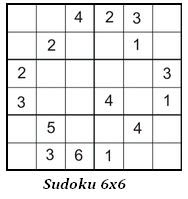
Sudoku

Sudoku, por vezes escrito Su Doku, é um quebra-cabeça baseado na colocação lógica de números. Seu formato é mais frequentemente uma grade de 9×9 constituída de sub-grades de 3×3 chamadas de regiões (outros termos incluem caixas, blocos, algumas vezes porém o termo quadrante é utilizado, apesar de ser um termo impreciso para uma grade de 3×3). Algumas células já contém números, chamadas como números dados (ou algumas vezes pistas). O objetivo é preencher as células vazias, com um número em cada célula, de maneira que cada coluna, linha e região contenham os números 1 a 9 apenas uma vez. Portanto, na solução do jogo, cada número aparece apenas uma vez em qualquer um dos sentido ou regiões, daí portanto "únicos números" originaram o nome do jogo ou enigma.

As possibilidades

 
O primeiro passo é analisar cada linha, coluna e célula e encontrar os números que poderiam ser colocados ali - ou seja, aqueles que ainda não existem em nenhuma dessas 3 posições. Comece sempre pelos grupos que têm mais números-pista já dispostos. O ideal é anotar todas as possibilidades a lápis, para poder ir apagando depois.

Tirando da reta

 
Nas casas em que só há uma possibilidade, você já tem o resultado. Escreva o número e exclua-o das outras casas que estejam na mesma linha, coluna ou célula. Repita o processo várias vezes, até preencher todo o quadrado. 

 


Níveis de dificuldade

A atração do jogo é que as regras são simples, contudo, a linha de raciocínio requerida para alcançar a solução pode ser complexa. O Sudoku é recomendado por alguns educadores como um exercício para o pensamento lógico. O nível de dificuldade pode ser selecionado para combinar com o público. A maioria das publicações classifica seus enigmas do Sudoku em quatro níveis de dificuldade, os títulos de alguns jogos são classificados de "fácil", "intermediário", "difícil", e "desafiador". Sudoku assim como na maioria dos outros enigmas de lógica pura, apresenta uma única solução possível. Existem diversas fontes na Internet não ligadas a editoras que disponibilizam os jogos gratuitamente.

História

 
O primeiro conceito do Sudoku foi criado no século XVIII pelo matemático suíço Leonhard Euler e recebeu o nome de Quadrados Latinos. Ninguém sabe direito de onde vem esse nome. Alguns acreditam que seja pelo fato de os latinos perderem a paciência muito rapidamente e o mesmo acontecer quando alguém se aventura nesse jogo. quando Euler perdeu a visão devido a catarata, ele passou a desenvolver a capacidade de fazer contas de cabeça com grandes números, além do talento de criar quebra-cabeças.

Os Quadrados Latinos ficaram aparentemente esquecidos até os anos 70, quando uma empresa americana redescobriu o jogo e lançou-o no mercado com o nome de Lugar dos Números, com pouco sucesso. Em 1984, a Nikoli, maior empresa japonesa de quebra-cabeças, descobriu o jogo e decidiu levá-lo àquele país. Dito e feito. O jogo foi primeiro introduzido no mercado japonês com o nome de “suuji wa dokushin ni kagiru”, que significa “os dígitos devem permanecer únicos”. Esse palavrão foi logo abreviado para duas simples palavras “Su”, que significa “número” e “Doku”, que é “único”.

Em 1986, depois de alguns aperfeiçoamentos no nível de dificuldade e na distribuição dos números, o sudoku tornou-se um dos jogos mais vendidos do Japão, onde os jogos numéricos são mais populares que palavras-cruzadas e caça-palavras, que não funcionam muito bem na língua japonesa. Wayne Gould havia criado um programa de computador que gerava jogos de sudoku com vários níveis de dificuldade e não estava cobrando nada por ele. Assim The Times decidiu arriscar e no dia 12 de novembro de 2004 publicou seu primeiro sudoku. No Brasil, o Sudoku é publicado pelas Revistas Coquetel (Ediouro) desde o início de 2005.

Diversidade

 
Apesar de a grade 9×9 com regiões 3×3 ser de longe a mais conhecida, diversas variações abundam: amostras do enigma podem ser formado por um quadrado bidimensional, dividido em 16 casas na versão 4x4, 36 casas na versão 6x6.

Boa sorte...

"A única saída é a capacitação"

Jeremy Kilpatrick

JEREMY KILPATRICK, Professor norte-americano, acredita que é necessário encontrar novas maneiras de preparar os docentes para que ajudem os alunos a raciocinar   

"Para melhorar o ensino de Matemática, 
não é necessário investir mais recursos, 
mas aprimorar os programas de formação." 

Modernização dos métodos de ensino, desempenho ruim em avaliações de Matemática e uso da calculadora na sala de aula. Essas questões preocupam não só professores brasileiros mas também os de países desenvolvidos, como os Estados Unidos. Jeremy Kilpatrick é um deles. Docente do Instituto de Educação em Matemática da Universidade da Geórgia, ele faz parte da Academia Nacional de Educação dos EUA e do grupo responsável pelo Education Policy White Papers, um relatório de recomendações em políticas educacionais. O estudo, que tem como destinatário o governo norte-americano, traz artigos elaborados por educadores com base nas pesquisas mais recentes com a missão de ajudar a entender quais os problemas atuais do sistema de ensino daquele país, apresentando sugestões para resolvê-los.

Kilpatrick afirma que quem leciona Matemática muitas vezes não conhece a matéria a fundo e, consequentemente, não consegue ensiná-la. "Para melhorar o quadro, não é necessário investir mais recursos, mas aprimorar os programas de formação", diz. Pesquisas no ensino da disciplina mostram que quem é bem qualificado sabe, por exemplo, como usar o computador como aliado na sala de aula, auxiliando os alunos a desenvolver o raciocínio. Em dezembro de 2008, a convite da Escola de Altos Estudos da Coordenação de Aperfeiçoamento de Pessoal de Nível Superior e da Uniban Brasil, Kilpatrick esteve em São Paulo para ministrar o curso Tendências em Educação Matemática e concedeu a seguinte entrevista a NOVA ESCOLA.

A Matemática ensinada nas escolas ao redor do mundo é ultrapassada?

JEREMY KILPATRICK: Em geral, a disciplina continua sendo trabalhada do mesmo modo que na época de nossos avós. O que ensinar, certamente, mudou, mas alterações no como fazer são mais difíceis de acontecer. Quem não domina o conteúdo acha mais fácil ensinar do jeito antigo porque sempre existe uma resposta no fim do livro, que pode ser usada mesmo sem a compreensão de como chegar a ela. Para que a turma avance, os professores precisam aplicar novos conceitos, o que é difícil se eles não conhecem os conteúdos. Isso é imprescindível para estimular as crianças a investigar e ter ideias, compreender o que estão querendo dizer e seguir a linha de raciocínio delas. Em sua maioria, os educadores não têm chance de se aprofundar na área. Por isso, eu acredito que o ensino acaba sendo muito tradicional não apenas nos Estados Unidos, mas também no Brasil e em muitos outros países.

Qual sua opinião sobre a interação entre os estudantes - com a formação de duplas ou grupos maiores?

A estratégia é boa. Em situações como essa, em vez de só ouvir o mestre falar o tempo todo, as crianças têm a oportunidade de ouvir a opinião dos colegas e responder a perguntas deles. Em grupos de dois, três, quatro e até cinco, elas não só encontram a resposta para um problema apresentado mas também aprendem a discutir o raciocínio. Se um integrante da equipe mostrou como chegou à solução e alguém não entendeu, cabe a ele descobrir uma maneira de explicá-lo. É necessário, no entanto, encontrar maneiras de avaliar pessoas em grupos. Se a estratégia está sendo usada em sala, ela deve ser repetida na hora da avaliação. Além do mais, esse é o modo como as pessoas trabalham atualmente no mundo real.

Como ajudar os jovens a se preparar para a sociedade de hoje, em que a tecnologia tem um papel central?

Se crianças e adolescentes usam o computador em casa, na escola eles deveriam utilizá-lo de forma mais inteligente não só para jogar games, mas para aprender Matemática e outras disciplinas. É possível, por exemplo, trabalhar a álgebra com o uso de planilhas, que ajudam a entender conceitos, encontrar padrões e perceber o que acontece quando algumas operações são realizadas. Além disso, ensinar a lidar com dados é primordial. Estatísticas e operações com números grandes são recorrentes no mundo do trabalho. Se ninguém faz isso a mão, por que insistir em que a criança o faça? Essas tarefas podem ser realizadas no computador, mas para entender o que os resultados significam é essencial conhecer Matemática - álgebra, estatística, probabilidade e geometria.

Os professores americanos já levam a tecnologia para a escola?

Sim. Eles acham muito positivo utilizar o computador em classe porque alguns programas possibilitam apresentar bons exercícios à turma. Eles também estão usando a calculadora, apesar de se preocuparem com a imagem negativa que ela tem. Em geral, acredita-se que, se recorre a esse equipamento, o aluno não está raciocinando.

E qual sua opinião sobre isso?

É importante que a calculadora faça parte do material escolar. Se um educador é bem formado em Matemática, deixa que a garotada recorra a ela. Nesse caso, o equipamento precisa ser aceito também nas provas. Ouvi que no Brasil isso não é permitido, o que não faz sentido. Quando esse recurso é empregado de maneira inteligente, o aluno se torna capaz de questionar, estimar e ser cético. Ele pensa: "Posso ter apertado o botão errado. Essa resposta é razoável?" Isso exige uma boa noção dos números e de como o cálculo é feito. A calculadora não é eficaz se a garotada não tiver desenvolvido essa capacidade.

O raciocínio das crianças mudou em decorrência do contato cada vez mais precoce com o computador?

O equipamento pode ter mudado a forma como elas pensam, mas ainda não entendemos de que maneira. Se isso de fato ocorreu, duvido que tenha sido prejudicial. Não acho que os computadores mudem o jeito de aprender Matemática ou lidar com ela. Há uma preocupação demasiada com o costume das crianças de usá-lo para coisas simples, que seriam facilmente feitas sem ele. É essencial aprender, por exemplo, a multiplicação de números pequenos - para a qual o computador não é essencial. Cabe ao professor encontrar formas de fazer com que os estudantes se lembrem do que deve ser memorizado, mas também ensinar a eles modos de usar o micro com inteligência, o que não afeta o raciocínio. Ao contrário, até ajuda.

Como um dos elaboradores do Education Policy White Papers - com recomendações ao governo sobre formas de melhorar a Educação nos Estados Unidos -, qual sua opinião sobre a disposição de Barack Obama para discuti-lo e fazer mudanças?

O presidente Obama afirma querer aprimorar o desempenho dos estudantes em Matemática e Ciências, mas não se sabe se a Educação estará na lista de prioridades dele porque os desdobramentos da crise econômica mundial ainda estão indefinidos. Há uma diferença entre o que o governo quer fazer em relação ao aumento da verba destinada à Educação e o que de fato vai fazer. Além disso, não há a certeza de que o Congresso ouvirá nossas recomendações, apesar de a Academia Nacional de Educação estar interessada em influenciar os deputados e senadores.

É possível para um país como o Brasil aumentar o nível de exigência com relação ao desempenho dos jovens em Matemática?

O ideal é estabelecer metas tão elevadas quanto possível e, então, fazer os encaminhamentos no sentido de atingi-las. A formação e as condições de trabalho podem ser melhoradas, e não é apenas mais dinheiro que vai tornar isso possível. A sociedade deve se convencer de que necessita de professores bem preparados para que a Educação melhore. Só assim vai consegui-los. É importante ainda descobrir quais programas de qualificação funcionam melhor e achar uma maneira de fazer com que preparem mais gente. Outro caminho é encontrar onde estão os profissionais bem qualificados e a razão pela qual eles são melhores que os demais.

Quais as características de um programa de formação eficiente?

Fiquei impressionado com algo que é feito na Alemanha. Os recém-formados têm muita ajuda nos dois primeiros anos de trabalho, que funcionam como uma extensão da formação. Durante esse período, os formadores checam como eles estão se saindo e dão auxílio. Alguns programas nos EUA estão começando a fazer isso.

Qual o país com o melhor ensino de Matemática atualmente?

Costuma-se dizer que é Cingapura. Eu estive lá e acho que o sistema é muito bom. Como o país é pequeno, todo o Magistério é preparado em uma mesma universidade e o Ministério da Educação consegue monitorar o desempenho de cada docente. Se um deles não está indo bem, o governo procura formas de ajudá-lo. O sistema dá apoio a todos, que são bem preparados e, acredito, bem pagos. O Japão também tem um bom sistema, em que a equipe de educadores se reúne e discute o que e como está ensinando. A Suíça e os países nórdicos também estão se saindo muito bem.

Como as pesquisas sobre didáticas específicas podem ser aplicadas?

Os programas de formação são muito curtos e não há tempo de cobrir tudo. Mas uma coisa a fazer é transformar essa qualificação em uma pós-graduação, que teria duração maior. No fim dessa preparação, os aprovados sairiam com um diploma e teriam aprendido como ensinar conteúdos específicos. Outro caminho - adotado em países como a Nova Zelândia - é colocar na internet para a consulta dos que têm dúvidas sugestões de como ensinar certos tópicos preparadas pelo Ministério da Educação ou algum grupo de pesquisa.

Um modelo que tem como foco levar os alunos a tirar boas notas em avaliações fora da escola é válido?

Não há como fugir disso. A solução é produzir avaliações muito boas e procurar um modo de permitir que os professores possam participar do processo. Na Alemanha, conheci uma iniciativa do governo que consistia em deixar que eles fizessem algumas das avaliações para as próprias turmas, que eram usadas como parte da nota do exame nacional. É claro que num caso como esse a checagem se torna essencial, mas o ponto é deixar que os docentes elaborem provas com base no que ensinam em sala de aula e fazer com que elas tenham algum peso. É difícil, mas possível.

O Brasil tem um histórico de desempenho ruim em avaliações de Matemática. Qual a razão para isso?

O Pisa (sigla em inglês para Programa Internacional de Avaliação de Alunos), que é o indicador mais usado, não é muito relacionado com o currículo, mas com o uso da Matemática no mundo. Ele é aplicado a jovens de 15 anos, não importando em que série estão. O objetivo é avaliar como eles conseguem se valer da Matemática para resolver problemas. Os brasileiros e norte-americanos, dizem os resultados, não sabem como utilizar o que aprenderam na escola. O Pisa requer raciocínio para a resolução de problemas complicados, o que eles não estão fazendo. O resultado negativo revela algo sobre o trabalho desenvolvido nas escolas.

Como mudar esse quadro?

É interessante que os pesquisadores analisem as respostas dadas às questões. Elas podem revelar algumas possibilidades: que os estudantes não estão entrando em contato com bons problemas, que o exame está muito distante do que estão aprendendo na escola e, por isso, eles desistem de tentar responder às questões ou de que os jovens simplesmente não estão levando o exame a sério. Não existe um incentivo para que eles se esforcem no Pisa, já que não recebem uma resposta sobre o desempenho que tiveram. Os professores, por sua vez, também não ficam sabendo como os alunos deles se saíram na prova. Se nada for feito com esses resultados, a avaliação não faz muito sentido.

Março 2009

 Paula Sato

Foto: Marcos Rosa

Fonte:http://revistaescola.abril.com.br/matematica/fundamentos/unica-saida-capacitacao-427743.shtml

Letra E

EIXO DE SIMETRIA - A reta que separa uma figura de sua reflexão ou rebatimento.

EIXOS - Quando se traça as coordenadas ou gráfico em 2 dimensões, usamos 2 eixos, x na horizontal e y na vertical. Quando no espaço existe mais um eixo perpendicular ao plano xy, o novo eixo é chamado de z.

EIXO DOS X - É o eixo horizontal em um sistema cartesiano ortogonal. Local onde são marcadas as abcissas de qualquer ponto.

EIXO DOS Y - É o eixo vertical em um sistema cartesiano ortogonal. Nesse eixo são marcadas as ordenadas.

EIXO DOS Z - É o eixo que tem representação no espaço e é perpendicular ao plano formado pelo os eixos dos x e dos y. Normalmente é apresentado na posição vertical.

ELEMENTO - Um objeto de um conjunto é um elemento deste conjunto.

ELEMENTO NEUTRO - Em uma operação é o elemento que não tem influência no resultado final. O elemento neutro na adição é o zero na multiplicação e divisão é o 1. Ex.: 5 + 0 =5 ; 7 x 1 =7.

ELIPSE - Curva plana em que a soma das distâncias de qualquer ponto a dois pontos chamados focos se mantêm constante.

ENEÁGONO - Um polígono com 9 lados.

ENUMERAR - Associar objetos de uma forma unívoca aos números naturais.

EQUAÇÃO - Expressão algébrica indicada por uma igualdade, onde há valores desconhecidos expressos por letras (incógnitas).

EQUAÇÃO EXPONENCIAL - Uma equação onde a incógnita figura como expoente.

EQUAÇÃO FRACIONAL - Uma equação onde a variável independente figura em denominador.

EQUAÇÃO LINEAR - É uma equação da forma ax + b = 0, onde a e b são números. Pode-se exprimir uma relação linear com a expressão y = ax + b que representa, em um sistema cartesiano, uma reta.

EQUIVALENTES - Que é do mesmo valor. Aquilo que equivale.

ESCALA - A razão que compara, em um mapa, a distância no mapa com a distância real.

ESFERA - Uma figura formada pelo conjunto de todos os pontos do espaço tridimensional, equidistantes de um ponto fixo denominado centro da esfera, por uma distância fixa conhecida como o raio da esfera.

ESQUADRO - Instrumento de desenho com a forma de um triângulo retângulo.

ESTATÍSTICA - Parte da Matemática que organiza e apresenta informações numéricas, além de obter conclusões a partir dessas informações.

ESTIMATIVA OU ESTIMAR - Atitude de estimar um resultado numérico. É o resultado aproximado de uma operação. Pode ser feito mentalmente ou por escrito. Embora saibamos que  π = 3,1415926535..., podemos fazer uma estimativa para o valor de Pi como sendo a divisão de 22 por 7.

EXPRESSÃO NUMÉRICA - Seqüência de operações numéricas indicadas, ou seja, não efetuadas.

EXCENTRINCIDADE - Razão usada em algumas definições de uma cônica.

3ª susseção

Observando a figura abaixo, qual o desenho que falta?

 Boa sorte!

Referência:

Lógica nas diagonais do quadrado

Destes quadrados, na figura abaixo, quatro pertencem à mesma família. Qual é o intruso?

 

Referência:

X ENEM

DIREITO

Com base nas leis e na Constituição do país, o advogado é o profissional legalmente habilitado para representar e defender os interesses de seus clientes em qualquer juízo ou tribunal e também nas questões não judiciais.

Sempre sujeito a um código de ética, o advogado é o único que pode elaborar e subscrever petições iniciais, contestar memoriais, razões, minutas e contraminutas em processos, entrar com habeas-corpus, recorrer nas decisões judiciais, fazer contratos e exercer defesa.

No entanto, para o exercício da profissão após a conclusão do curso, é necessário fazer estágio e submeter-se a um exame da OAB - entidade que exerce função de fiscalizadora da capacitação dos profissionais da área.
O bacharel em Direito pode dedicar-se à área jurídica, tornando-se delegado de polícia, promotor de justiça ou juiz de Direito. Como promotor, elabora pedido, contestações, réplicas, memoriais. Na área de magistratura, pode atuar como juiz, desembargador ou ministro. O ingresso nessas carreiras é feito através de concurso público.

Há, ainda, outras opções para o advogado, como trabalhar em assessoria e consultoria jurídica de empresas públicas e privadas ou o magistério superior, caso escolha a carreira acadêmica.

A matemática possui um papel complementar - porém importante no dia-a-dia desse profissional quando trabalha com causas que envolvem bens, valores, partilhas e heranças.

Referência:

Machado, Antônio dos Santos. Matemática na escola do 2º grau - Vol 1. S. Paulo: Atual, 1996

MEDICINA

A medicina é a ciência que está mais diretamente ligada à vida. Responsável pela prevenção, detecção e cura das doenças - físicas e psicológicas - que acometem os seres humanos, os médicos, podem se valer, hoje, de diversos avanços tecnológicos e científicos que propiciam a descoberta da cura de muitos males.

As atividades desse profissional estão diretamente relacionadas ao estudo dos fenômenos biológicos do organismo humano, à pesquisa de novos tratamentos e medicamentos e aos exames clínicos de modo geral.
Ao contrário do que acontecia em outros tempos, dispomos hoje de um grande números de profissionais especializados no tratamento de um órgão ou de um sistema de órgãos - o que permite maior aprofundamento e maior conhecimento sobre todos os mecanismos que compõem o corpo humano.
A medicina forma profissionais especializados em pediatria, ginecologia e obstetrícia, oftalmologia, anestesiologia, cirurgia e ortopedia, clínica médica, dermatologia, radiologia, neurologia, psiquiatria, medicina legal, saúde pública, patologia, entre outros ramos.

O médico esta apto para trabalhar em hospitais, clínicas, casas de saúdes, sanatórios, escolas, laboratórios, instituições públicas ou recreativas, instituições cientificas e de pesquisas. Pode, ainda exercer atividade liberal montando clínica própria.

A matemática esta presente nessa atividade - tão antiga quanto diversificada - e muito contribui para o seu desenvolvimento. Apesar de os médicos não necessitarem do conhecimento pleno dessa ciência, necessitam de conhecimentos inter-relacionados de estatísticas, física e matemática, para que possam alcançar bons resultados em seu trabalho.

Referência:

Machado, Antônio dos Santos. Matemática na escola do 2º grau - Vol 1. S. Paulo: Atual, 1996.

Oração Matemática I

Mestre matemático que estais na sala, 

Santificada seja a Vossa prova, 

Seja de Álgebra ou de Geometria,

O zero de cada dia não nos dai hoje, 

Perdoai as nossas bagunças, 

Assim como perdoamos os Vossos Teoremas, 

Não nos deixeis cair em recuperação, 

Mas nos livrai da reprovação, 

Amém.

Referêncial:

Site: Cálculu's

Símbolo de Multiplicação "×"

O símbolo de multiplicação  × (xis ou vezes) pode também ser representado por:

• ou por · (um ponto situado a meia altura)
• ou um * (asterisco)

Ou seja:

5 × 4  = 5 · 4 = 5 * 4

O sinal do produto deriva da utilização do símbolo da cruz de San Andrés para os cálculos de proporções na antiguidade. O clérigo inglês William Oughtred, que viveu entre fins do Século XVI e princípios do XVII, usou este símbolo e o propôs, entre muitos outros, para designar as operações de multiplicação, empregou-o pela primeira vez, no livro Clavis Matematicae publicado em 1631.

Ainda em 1631, Harriot, para indicar também o produto a efetuar, colocava um ponto entre os fatores. Em 1637, Descartes já se limitava a escrever os fatores justapostos, indicando, desse modo abreviado, um produto qualquer. Contudo, o ponto foi introduzido como um símbolo para a multiplicação por Leibniz. Julho em 29, 1698, a qual  escreveu em uma carta a John Bernoulli:

"eu não gosto de × como um símbolo para a multiplicação, porque é confundida facilmente com ×; freqüentemente eu relaciono o produto entre duas quantidades por um ponto ".

Assim, Leibniz decidiu utilizar o ponto simples para indicar multiplicação "·", que também se utiliza na atualidade para o produto. De acordo, a Venturi, o simbolo "×" é provável que seja originário de uma alteração do símbolo de +.

O asterisco que é usado frequentemente em computação pois está presente em praticamento todos os tipos de teclado. O sinal do asterisco vem da linguagem de programação FORTRAN, uma linguagem de máquina desenvolvida a partir da década de 1950 e que continua a ser usada hoje em dia, porém,  o asterisco não é usado quando escrevemos matemática à mão, pois não é um símbolo matemático mas sim um operador de multiplicação.

Referência:

Site: Só Matemática

Venturi, Jacir J. Álgebra Vetorial e Geometria Analítica. 9º ed. Curitiba-PR.

Tycho Brahe

Brahe

Brahe, Tycho (1546-1601)

Durante os 55 anos de sua vida, Tycho Brahe viveu como astrônomo revolucionário e matemático, mas numa existência repassada de romance, aventura, astrologia, alquimia, fanfarronadas e charlatanice. Ainda assim, sua contribuição para o progresso da Ciência, em seu tempo, iria influenciar os trabalhos mercantes de Galileu e Kepler. 

Tão acuradas foram suas observações astronômicas que, ainda hoje, com todos os modernos recursos ópticos e computadores, os astrônomos consultam suas Tábuas Rudolfinas para saber qual teria sido a posição de Marte em determinada época. Foi Brahe, também, o primeiro astrônomo a levar em conta a refração atmosférica na determinação das posições dos astros, numa época em que não se dispunha sequer do telescópio.

Primogênito numa prole de dez irmãos, Brahe não poderia divisar largos horizontes na obscura província dinamarquesa de Schonen (Scania), onde nasceu. O pai, um advogado que exercia o cargo de governador de um departamento, desfrutava de posição mais honorífica que rendosa. Mesmo os recursos do tio abastado e sem filhos, que assumiu sua tutela, só prometiam a Tycho a esterilidade de uma carreira sem emoções: o tio insistia para que ele se dedicasse ao estudo das leis.

Durante seus estudos de astronomia nas Universidades aconteceu um fato curioso: Em uma discussão encarniçada com Brahe sobre um problema matemático um outro estudante fê-lo perder o nariz num duelo a espada. A partir de então,  Brahe foi obrigado a usar maquiagem para dissimular, em virtude de uma prótese metálica.

Além de ser astrônomo Brahe estudou alquimia e astrologia. Ele construiu um observatório astronômico em uma ilha nas proximidades de Copenhagen com o apoio do rei da Dinamarca. Brahe registrou cuidadosamente mais de vinte anos de observações astronômicas precisas.

Após seu trabalho de observação, tornou-se matemático do Império em Praga. Kepler era seu assistente. Brahe acreditava que suas informações comprovariam sua crença de que a Terra era o centro do universo. Mais tarde, Kepler utilizou as informações para deduzir suas leis planetárias e provar que o Sol era o centro do universo.

Referência:

Site: Guia para a história do cálculo (complemento dos texto da 10ª edição do livro de Cálculo do Thomas)

Site: Wikipédia

François Viete

Viete

Viete, François (1540-1603)

François Viète nasceu em Fontenay, França. Estudou direito na Universidade de Poitiers e passou muito de seu tempo estudando matemática e criptografia enquanto mantinha uma carreira bem-sucedida como advogado. Mais tarde ele aplicou a trigonometria básica à astronomia e escreveu Harmonicum coeleste. 

Em 1579 publicou Canon mathematicus seu ad triangula. Mais tarde concentrou seus esforços em álgebra e geometria. Publicou In artem analyticem isagoge em 1591 e Supplementum geometriae em 1593. Essas obras foram as primeiras a introduzir a notação algébrica simbólica e as técnicas para ângulos trissecados. 

Ele simplificou a notação da álgebra e foi um dos primeiros a utilizar letras para representar números. Seu livro De aquationum recognitione et emendatione foi publicado apenas após sua morte. Ele continha a teoria das equações, incluindo metódos para resolução das polinomiais de segundo, terceiro e quarto graus e a introdução dos termos negativo e coeficiente.        

É conhecido como o pai da álgebra moderna porque foi o primeiro a usar letras para representar variáveis. Além disto, este matemático foi também um dos melhores criptoanalistas da sua época, pois, segundo a história, Viéte conseguiu quebrar um código secreto usado pela Espanha, formado por, aproximadamente, 600 caracteres, conseguindo com isto uma vantagem para seu país na guerra travada contra a Espanha durante dois anos. O rei Felipe II da Espanha estava tão seguro de seu código secreto que acusou Viéte de que a França estava usando magia contra seu país.

Principais obras: 

Harmonicum coeleste;   
Canon mathematicus seu ad triangula;  
De aquationum recognitione et emendatione; 
Artem analyticem isagoge; 
Supplementum geometriae.

Referência:

Site: Guia para a história do cálculo (complemento dos texto da 10ª edição do livro de Cálculo do Thomas)

Site: Wikipédia

Sequência numérica IV

Determine os próximos número da sequência:

1 - 1
8 - 4
  9 - 27
64 - 16
  25 - 125
? - ?

Referência:

Mão na forma - A espiral e as proporções áureas

Mão na forma - Nas malhas da Geometria

Mão na forma - Diálogo geométrico

Mão na forma - Quadrado, cubo e cia

Mão na forma - 3,4,5 e o pentágono

Mão na Forma - Os Sólidos de Platão

Tijolo e meio

Um tijolo pesa tanto quanto 1 quilograma mais meio tijolo. Quanto pesa um tijolo e meio?

Os 21 vasos

Dividir 21 vasos por três pessoas, sendo 7 cheios de vinho, 7 meio cheios de vinho e 7 vazios, de forma que cada pessoa receba o mesmo número de vasos e mesmo volume de vinho, sem alterar o conteúdo dos vasos.

Referência: 

 

TAHAN, Malba. O homem que calculava. 64ºEd. Rio de Janeiro: Record, 2003.